El seguimiento de objetos es una tarea importante dentro del campo de computer vision. En este post consideramos la metodología de object tracking conocida como tracking-by-detection donde los resultados de la detección de objetos se dan en cada frame como input y el objetivo es asociar las detecciones para encontrar las trayectorias de los objetos. No se puede esperar que se detecten todos los objetos en cada frame, puede haber falsas detecciones y algunos objetos pueden ser ocluidos por otros; estos factores hacen que la asociación de datos sea una tarea difícil.
Comenzamos revisando el problema tracking-by-detection, siguiendo de cerca la formulación utilizada en [1, 2]. Asumimos la existencia de \(z^{(i)}_t\), que corresponde a la detección \(i\) realizada en el tiempo \(t\). Notese que no se especifica la forma de la detección (por ejemplo, bounding box, feature vector, trazas de optical-flow, etc). Denotamos el conjunto de todas las detecciones en un video como \(\mathbf{Z}\). Además, definimos una track \(\mathbf{x}^{(k)} = \{z^{(i)}_{t_0}, \cdots, z^{(i)}_{t_{T_k}}\}\) como una lista ordenada de detecciones que contiene toda la información necesaria para rastrear un objeto incluyendo, pero no limitándose, a su ubicación actual. Estos tracks codifican los cambios que experimenta el objeto \(k\) desde el momento de su primera detección efectiva hasta la última, proporcionando la noción de persistencia necesaria para distinguir los objetos entre sí dentro de un vídeo. Definimos el conjunto de todos los tracks como \(\mathbf{X} = \{ \mathbf{x}^{(1)}, \cdots, \mathbf{x}^{(K)}\}\).
Utilizando la formulación de tracking-by-detection, pretendemos maximizar la probabilidad posterior de \(\mathbf{X}\) dado \(\mathbf{Z}\), como
\(\begin{aligned}
\operatorname*{max}_\mathbf{X} p(\mathbf{X} \vert \mathbf{Z}) & = \operatorname*{max}_\mathbf{X} p( \mathbf{Z} \vert \mathbf{X}) p(\mathbf{X}) \\
& = \operatorname*{max}_\mathbf{X} \prod_{i,t} p(\mathbf{z}^{(i)}_{t} \vert \mathbf{X}) \prod_{k} p(\mathbf{x}^{(k)}),
\end{aligned}
\tag{1}\label{1}\)
donde asumimos independencia condicional entre detecciones dada una colección de tracks; e independencia entre los tracks, esto significa que el movimiento de cada objeto es independiente. Es difícil optimizar la ecuación anterior directamente, porque el espacio de \(\mathbf{X}\) es enorme, sin embargo, podemos reducir el tamaño del espacio de búsqueda utilizando la observación de que un objeto sólo puede pertenecer a una trayectoria. Esto se traduce en la restricción de que los tracks no puede superponerse entre sí, es decir, \(\mathbf{x}^{(k)} \cap \mathbf{x}^{(l)} = \varnothing \mbox{ }, \forall k \neq l\). Asumimos además que las transiciones de tracks siguen un modelo de Markov de primer orden \(p(\mathbf{x}^{(k)}) = p(x^{(k)}_{t_0}) \prod_{t} p(x^{(k)}_{t_{l}} \vert x^{(k)}_{t_{l-1}})\).
La ecuación \(\eqref{1}\) muestra que el problema de tracking-by-detection puede descomponerse en dos sub-problemas: evaluar la probabilidad de las detecciones \(p( \mathbf{Z} \vert \mathbf{X})\) (por ejemplo, modelarlas en terminos de apariencia, forma, y evaluar la necesidad de nuevos tracks) y modelar los tracks \(p(\mathbf{x}^{(k)})\).
Tipos de object tracking
Partiendo de la ecuación \(\eqref{1}\) y de las asunciones anteriores, se puede modelar el problema de tracking-by-detection de dos formas concidas en la literatura como las formulaciones batch y online.
Metodos online como [2, 3] asocian las detecciones del frame entrante inmediatamente a las trayectorias existentes y, por lo tanto, son apropiadas para aplicaciones en tiempo real, asimismo las trayectorias son modeladas como linear state space models, por ejemplo filtros de Kalman o filtros de particulas. La asociación a las detecciones en el frame actual se formula a menudo como un problema de asignacion binaria y se resuelve mediante el algoritmo húngaro.
Metodos batch como [1, 4] consideran observaciones pasadas, presentes y futuras o incluso toda la secuencia a la vez. Aunque no es aplicable en tiempo real, la ventaja de los métodos batch es el contexto temporal, que permite realizar predicciones más robustas. Una solución elegante para asignar trayectorias a las detecciones es la formulación network flow introducida en [1].
Batch object tracking
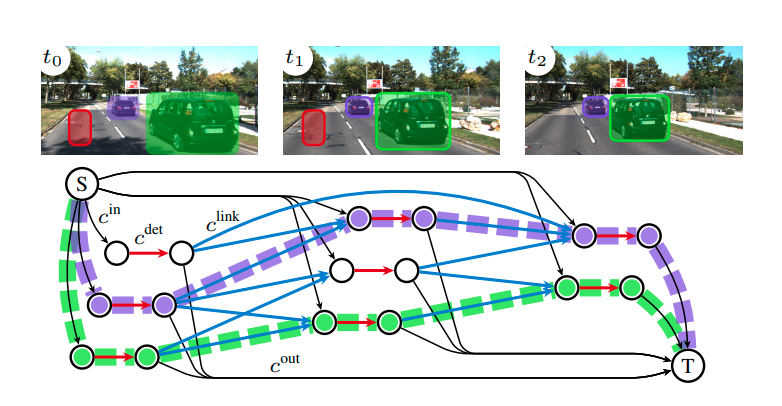 Figura 1: Un gráfico de flujo de red para el seguimiento de 3 tracks.
Figura 1: Un gráfico de flujo de red para el seguimiento de 3 tracks.
Los metodos batch se pueden representar como un grafo (Ver Fig. 1; tomada de [4]) donde cada detección \(\mathbf{z}_t\) se representa con dos nodos conectados por un borde (en rojo en la imagen). A este borde se le asigna la variable de flujo \(y^{det}_{t}\). Para poder asociar dos detecciones que pertenecen a la misma trayectoria \(\mathbf{X}\), se añaden al gráfico bordes dirigidos (en azul en la imagen) de todos los \(\mathbf{z}_t\) a todos los \(\mathbf{z}_{t'}\) tal que \(t < t'\) y \(\vert t - t'\vert < \tau_t\). A cada uno de estos bordes se le asigna una variable de flujo \(y^{link}_{t, t'}\). El hecho de tener bordes en múltiples frames permite manejar oclusiones o detecciones fallidas. Para reducir el tamaño del gráfico, eliminamos bordes entre las detecciones que están espacialmente distantes, esto lo que la variable \(\tau_t\) representa. Esta elección se basa en la suposición de los objetos de mueven aproximandamente con movimiento rectilineo uniforme en instantes cortos de tiempo. Para manejar el nacimiento y la muerte de las trayectorias, se añaden dos nodos especiales al gráfico. Un nodo fuente (\(S\)) que se conecta con el primer nodo de cada detección con un borde (negro en la imagen) al que se le asigna la variable de flujo \(y^{in}_t\). Asimismo, el segundo nodo de cada detección está conectado con un nodo de sumidero (\(T\)) y al borde correspondiente (negro) se le asigna la variable \(y^{out}_t\). Cada variable del gráfico está asociada a un costo. Para cada uno de los cuatro tipos de variables definimos el costo correspondiente, es decir, \(c^{in}_t = -\text{log } p(x^{(k)}_{t})\), \(c^{out}_T = -\text{log } p(x^{(k)}_{T})\), \(c^{det}_t = -\text{log } p( \mathbf{z}_{t} \vert \mathbf{X})\) y \(c^{link}_{t, t'} = -\text{log }p(x^{(k)}_{t} \vert x^{(k)}_{t'})\), que resulta de aplicarel logaritmo a la ecuación \(\eqref{1}\) y cambiar el problema de maximizacion a uno de minimizacion introduciendo un signo menos. Esto nos deja con el siguiente problema de programacion lineal conocido como Minimum-cost flow:
\(\begin{aligned}
& {\text{min}}
&& z = \displaystyle\sum_{\mathbf{x}^{(k)} \in \mathbf{X}} \left( c^{in}_{t_0} y^{in}_{t_0} + c^{out}_{t_{T_k}} y^{out}_{t_{T_k}} + \sum_{l>0} c^{link}_{t_{l+1}, t_{l}} y^{link}_{t_{l+1}, t_{l}} \right) + \sum_t c^{det}_t y^{det}_{t} \\
&&& z = \sum_{t} c^{in}_{t} y^{in}_{t} + \sum_{t} c^{out}_{t} y^{out}_{t} \sum_{t, t'} c^{link}_{t, t'} y^{link}_{t, t'} + \sum_{t} c^{det}_t y^{det}_{t} \\
&\text{s.t.}
&& y^{in}_{t} + \sum_{t'} y^{link}_{t, t'} = y^{det}_{t}\\
&&& y^{out}_t + \sum_{t'} y^{link}_{t, t'} = y^{det}_{t} \\
&&& y^{in}_{t}, y^{link}_{t, t'}, y^{out}_t, y^{det}_{t} \in \{0, 1\} \\
\end{aligned}\)
Encontrar la hipótesis de asociación óptima \(\mathbf{X}^\star\) es equivalente a enviar el flujo de la fuente \(S\) al sumidero \(T\) que minimiza el costo. Cada trayectoria de flujo puede ser interpretada como la trayectoria de un objeto, la cantidad de flujo enviada de \(S\) a \(T\) es igual al número de trayectorias de objetos en el video, y el costo total del flujo corresponde al loglikelihood de la hipótesis de asociación. Las restricciones de conservación del flujo garantizan que ningún flujo comparta un borde común y, por lo tanto, que no se superpongan las trayectorias.
Online object tracking
Los metodos online toman un enfoque greddy optando por resolver el problema de tracking-by-detection para cada frame, es decir, en \(t=0\) todas las detecciones \(z^{(i)}_0\) se asumen correctas y correspondientes a objetos distintos, y se las asocia con un track para cada detecion (este paso, aunque restrictivo es necesario para inicializar la solucion), luego una variante recursiva de la ecuación \(\eqref{1}\) es resuelta:
\(\begin{aligned}
& \operatorname*{max}_{\mathbf{X}} p(\mathbf{X}_t \vert \mathbf{Z}_{t}, \mathbf{X}_{t-1}^{\star})
\end{aligned}
\tag{2}\label{2}\)
La detección de objetos obtiene las detecciones \(\mathbf{Z}_{t}\) aplicando un detector pre-entrenado en el frame \(t\). Luego se encuentran las asociaciones óptimas entre \(\mathbf{Z}_{t}\) y \(\mathbf{X}_{t-1}^{\star}\) para formar la estimación actual de las trayectorias \(\mathbf{X}_t\) [5]. Notese que los tracks obtenidos utilizando el proceso definido por la ecuación \(\eqref{2}\) no son necesariamente óptimas en cuanto a la maximización de la distribución definida por la ecuación \(\eqref{1}\). Dado que el número de todas las enumeraciones posibles de \(\mathbf{X}_t\) dadas las trayectorias optimas \(\mathbf{X}_{t-1}^{\star}\) encontradas en \(t-1\) y las detecciones \(\mathbf{Z}_{t}\) es enorme, resolver directamente la ecuación \(\eqref{2}\) es intratable.
Simplificamos aun mas es problema resolviendo únicamente un problema de asociación de datos entre \(\mathbf{X}_{t-1}^{\star}\) y \(\mathbf{Z}_{t}\), para luego obtener las trayectorias óptimas \(\mathbf{X}_t^{\star}\) actualizando \(\mathbf{X}_{t-1}^{\star}\) con las detecciones asociadas. Hacemos esto definiendo una matriz de asignación \(\Psi = [\Psi_{i,j}]_{n \times m}\) para representar la asociación entre \(\mathbf{X}_{t-1}^{\star}\) y \(\mathbf{Z}_{t}\) , donde cada entrada \(\Psi_{i,j} \in \{0,1\}\) indica si la detección \(j\)-esima está asociada a la trayectoria \(i\)-esima o no. Luego, el problema de la asociación de datos se expresa como un problema de estimacion MAP
\[\begin{aligned}
\Psi^{\star} & = {\text{argmax}} \displaystyle\sum_{i,j} \Psi_{i,j} \text{log } p(\Psi_{i,j}=1 \vert \mathbf{Z}_{t} \mathbf{X}_{t-1}), \\
\text{s.t.} & \displaystyle\sum_{i} \Psi_{i,j} = 1 \mbox{ }, \forall j \\
& \displaystyle\sum_{j} \Psi_{i,j} = 1 \mbox{ }, \forall i
\end{aligned}\]
donde \(p(\Psi_{i,j}=1 \vert \mathbf{Z}_{t} \mathbf{X}_{t-1})\) es la probabilidad de asociación posterior cuando la detección \(j\)-esima se asocia a la trayectoria \(i\)-esima. Asumimos que las asociaciones de todos los pares de trayectoria y detección son independientes. La tarea es buscar la asignación óptima \(\Psi^{\star}\) que maximiza la probabilidad de asociación posterior.
Varios tipos de trackers pueden existir dependiendo de como modelemos la probabilidad de asociación posterior \(\text{log } p(\Psi_{i,j}=1 \vert \mathbf{Z}_{t} \mathbf{X}_{t-1})\), uno de los mas importantes es el Kalman tracker que aproxima la probabilidad de asociacion con la distancia de Mahalanobis \((\mathbf{z}^{(i)}_{t} - \mathbf{x}^{(j)}_{t})^{\intercal} \Sigma^{-1}_{t} (\mathbf{z}^{(i)}_{t} - \mathbf{x}^{(j)}_{t})\) o la medida de IoU (Intersection over Union) entre las detecciones y los tracks.
La distancia IOU entre las detecciones y los tracks maneja implícitamente la oclusión a corto plazo causada por los objetos dado que favorece adecuadamente las detecciones con una escala similar. Esto permite que tanto el objeto oclusor se corrija con la detección mientras que el objeto cubierto no se ve afectado por la falta de asignación. Asimismo cuando se usa la distancia de Mahalanobis, la matriz \(\Sigma\), que es la matriz de incertidumbre obtenida del filtro de Kalman, provee las siguientes ventajas: (1) la asignación de tracks a detecciones lejanas se vuelve improbable; y (2) la oclusión a corto plazo puede ser manejada cuando la incertidumbre de movimiento es baja.
¿Cómo se evalua el object tracking?
Existen muchas metricas para evaluar los resultados de un tracker, y la elección de la “correcta” depende en gran medida de la aplicación, ademas la búsqueda de una métrica de evaluación única y general es un problema abierto. Por un lado, es deseable resumir el rendimiento en un solo número que permita una comparación directa. Por otro lado, no se debe perder información sobre los errores individuales cometidos por los algoritmos pero proporcionar varias estimaciones de rendimiento impide una clasificación clara. Las metricas más comunmente usadas son:
- MOTA: Exactitud de seguimiento de múltiples objetos. Esta medida combina tres fuentes de error: falsos positivos, objetivos perdidos e identity switches (Más es mejor).
- MOTP: Precisión de seguimiento de múltiples objetos que mide la desalineación entre los bounding boxes anotados y los pronosticados (Más es mejor).
- IDF1: La proporción de detecciones correctamente identificadas sobre el número promedio de detecciones verdaderas (Más es mejor).
- MT: Mostly tracked que mide la proporción de trayectorias verdaderas que están cubiertas por una hipótesis de seguimiento durante al menos el 80% de su respectiva vida (Más es mejor).
- ML: Mostly lost que mide la proporción de trayectorias verdaderas que están cubiertas por una hipótesis de seguimient cuanto mucho el 20% de su respectiva vida (Menos es mejor).
- FP: El número total de falsos positivos (Menos es mejor).
- FN: El número total de falsos negativos (Menos es mejor).
- ID Sw.: El número total de cambios de identidad que es cuando se le asignado un ID a un track y este cambia repentinamente (Menos es mejor).
Implementando online object tracking
Para parte final del post, se implementa un online object tracker puramente basado en la apariencia de los objetos, el tracker resultante es muy similar al implementado en [6] (Notese que los resultados presentados aqui, no reflejan de ninguna forma los resultados que obtendria el metodo en [6]).
El dataset
Existen varios dataset que son la norma para el object tracking, entre estos los mas usados son MOT16, KITTI, y DETRAC1. Estos datasets son sumamente dificiles y reflejan las alta complejidad del problema de Object Tracking, ninguno de los datasets ha sido resuelto en su totalidad, por ejemplo, la entrada con MOTA mas alto en el dataset MOT16 es de 62.0 y de 30.7 en DETRAC, ambos métodos batch que incluyen alguna forma object re-identification y detectores de objetos sumamente poderosos. Para este post nos limitamos a una version muy limitada del problema que incluye detectiones perfectas y objetos que nunca dejan la escena, ni nuevos objetos que entran a la escena. Las únicas dificultades de este dataset son la oclusión, los objetos cambian de tamaño y rotan mientras se mueven, y el hecho de que los objetos son muy similares entre si. Este dataset que llamaremos BaseTracking, los componen digitos del dataset MNIST y ICONS8 que son parte de los benchmarks clásicos para probar algoritmos de clasificación. Los objetos del dataset propuesto se mueven de forma aleatoria en una escena estatica. Este es un ejemplo de un dato de BaseTracking:
| Training set |
Testing set |
 |
 |
La arquitectura
 Figura 2: Arquitectura usada para la asosiacion de deteciones y tracks.
Figura 2: Arquitectura usada para la asosiacion de deteciones y tracks.
Para intentar resolver el problema propuesto, reemplazamos el problema de asociacion por una red neuronal (Ver Fig. 2) que usa graph neural networks y que aprende conjuntamente la apariencia de los objetos y sus asociaciones comparando los tracks con las detectiones. El modelado de la apariencia usando redes neuronales profundas permite aprender características jerárquicas de los objetos y sus alrededores en múltiples niveles de abstracción. La red neuronal propuesta (que esta basada en el trabajo de [7]) estima las asociaciones entre los objetos en un par frames bajo exhaustivas permutaciones de sus features, esto limita un poco la escalibildad del metodo dado que el numero maximo de objectos que se pueden analizar es un dato que se debe dar a apriori. El modelo propuesto no asume que los pares frames de entrada aparecen consecutivamente en un vídeo. Esto promueve la robustez contra las oclusiones. La arquitectura exacta de la red tanto como los codigos que se usaron en este proyecto se pueden encontrar en este aquí.
Para enternar esta red neuronal de da como input las imagenes de detectiones en los frames \(I_t\) y \(I_{t \pm n}\), como funcion de perdida de busca minimizar la diferencia entre el output \(\hat{\Psi}_{i,j}\) y las asociaciones reales \(\Psi_{i,j}\) para esto de ulizan 3 de las 4 funciones de perdidas definidad en [6]. El Forward-direction loss (\(\mathcal{L}_f\)) que fomenta la correcta asociación de la imagen de \(I_{t \pm n}\) con \(I_t\), para calcularlo primero se aplica un softmax a las filas de \(\hat{\Psi}_{i,j}\) y luego aplica la funcion de perdida binary cross entroy. El Backward-direction loss (\(\mathcal{L}_b\)) que fomenta la correcta asociación de la imagen de \(I_t\) con \(I_{t \pm n}\), para calcularlo primero se aplica un softmax a las columnas de \(\hat{\Psi}_{i,j}\) y luego aplica la funcion de perdida binary cross entroy. El Consistency loss (\(\mathcal{L}_c\)) que limita las dicrepancias entre \(\mathcal{L}_f\) y \(\mathcal{L}_b\), y basicamente fomenta a la red neuronal a entontrar soluciones que satisfagan las restricciones del problema de asociacion, para calcularla se utiliza la funcion de perdida mean square error entre el softmax a las columnas y el softmax a las filas de \(\hat{\Psi}_{i,j}\). La funcion de perdidad final es la combinacion convexa de las tres funciones de perdida: \(\frac{\mathcal{L}_f + \mathcal{L}_b + \mathcal{L}_c}{3}\).
Resultados
Para comparar nuestro object tracker usamos el tracker definido en [3] como baseline a este los llamaremos Kalman tracker porque utiliza filtros de Kalman para modelar el movimiento de los objetos, mientras que a nuestro tracker los llamaremos DAT que significa deep association tracker. La evaluacion se realizo usando 100 datos del testing set y utilizando la libreria py-motmetrics. Los resultados se resumen en la siguiente tabla:
| Tracker |
MOTA |
MOTP |
IDF1 |
MT |
ML |
FP |
FN |
ID Sw |
| Kalman |
74.09% |
86.23% |
27.73% |
284 |
216 |
22 |
10239 |
2693 |
| DAT |
63.03% |
99.6% |
38.1% |
500 |
0 |
0 |
0 |
18484 |
| Tabla 1: Resultados obtenidos |
Se puede observar en la Tabla 1 que nuestro metodo supera en todas las metricas al Kalman Tracker a excepcion de cambios de identidad (ID Sw), dado que esta metrica da bastante peso al MOTA nuestro metodo obtiene un MOTA mas bajo que el baseline.
Referencias
[1] Zhang, L., Li, Y., & Nevatia, R. (2008, June). Global data association for multi-object tracking using network flows. In 2008 IEEE Conference on Computer Vision and Pattern Recognition (pp. 1-8). IEEE.
[2] Cobos, R., Hernandez, J., & Abad, A. G. (2019, June). A fast multi-object tracking system using an object detector ensemble. In 2019 IEEE Colombian Conference on Applications in Computational Intelligence (ColCACI) (pp. 1-5). IEEE.
[3] Bewley, A., Ge, Z., Ott, L., Ramos, F., & Upcroft, B. (2016, September). Simple online and realtime tracking. In 2016 IEEE International Conference on Image Processing (ICIP) (pp. 3464-3468). IEEE.
[4] Schulter, S., Vernaza, P., Choi, W., & Chandraker, M. (2017). Deep network flow for multi-object tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 6951-6960).
[5] Yang, M., Pei, M., & Jia, Y. (2020). Online maximum a posteriori tracking of multiple objects using sequential trajectory prior. Image and Vision Computing, 94, 103867.
[6] Sun, S., Akhtar, N., Song, H., Mian, A. S., & Shah, M. (2019). Deep affinity network for multiple object tracking. IEEE transactions on pattern analysis and machine intelligence.
[7] Kipf, T., Fetaya, E., Wang, K. C., Welling, M., & Zemel, R. (2018). Neural relational inference for interacting systems. arXiv preprint arXiv:1802.04687.
comments powered by